Theoretical Probability Of Winning Craps
- Theoretical Probability Of Winning Craps Against
- Theoretical Probability Of Winning Craps Games
- Theoretical Probability Of Winning Craps Rules
- Theoretical Probability Of Winning Craps Odds
ANATOMY OF A BANKROLL MURDER: HOW IT HAPPENS
In Part 1, I explained why the theoretical becomes reality and why you can’t avoid the theoretical house edge. Let’s now look at how the typical loss happens and then add the element of tilt to our play. Note: if you only want to see the final numbers, look to the bold text. I included the explanations so that you may double check and critique my math, if you are so inclined.
The logic is that if my pass line loses, I still win $7 from the Any Craps win. This looks good on paper, because I only lose $3 instead of $10 thanks to the Any Craps hedge. Furthermore, I only lose $1 if any number other than 2, 3, or 12 are tossed. There may be technical problems with getting accurate values for these numbers, but at its core, the formula for theo is simple: The theoretical win for players who play Casino War is (0.0290) × (total amount wagered). The theoretical win from players who place a wager on the pass line in craps is (0.0141) × (total amount wagered). The theoretical win from players who place a wager on the pass line in craps is (0.0141) × (total amount wagered). As a specific example, if players wager $1 per spin on roulette, for one million spins, the house expects to earn about 0.0526 × $1,000,000 = $52,600. Some players will win big in a session, other will lose big.
Tilt: what is it?
First, let’s discuss this issue of tilt. It’s broader than you may think.
Tilt is simply any stimulus that causes a gambler to deviate from his normal play. It’s really that simple and broad. While most people associate tilt with loser’s tilt – where a gambler chases after his loses by increasing his bets or making more bets – there are many forms of tilt.
All the forms of tilt also have a similar element in common: they compel the player to bet more, exposing more of his bankroll to the house edge. Here are some forms of tilt.
Winner’s tilt
Winner’s tilt is when the high and rush of winning compels the bettor to bet more. Winner’s tilt has the same effect as loser’s tilt in that the player will bet more because he is winning. Winner’s tilt also has the added danger of causing the player to start wasting his bankroll away from the table. Tilt doesn’t always just end when the player leaves the table.
FOMO tilt
There is what I call FOMO tilt, meaning the Fear Of Missing Out, where the bettor starts making bets because he is afraid of missing out on a win. The player normally would not make these bets, but since he’s already been making the bet, he must continue making the bet. He is afraid that once he stops, it might just hit. He has a fear of missing out.
Frustration Tilt
Our player is place betting the inside numbers and the outside numbers are hitting. Joe Gambler then switches to the outside numbers, and the inside numbers start hitting. Out of frustration, he now bets across, which is something he usually does not do.
It’s not wining or losing that’s setting off the gambler, it’s frustration.
Alcohol Induced Tilt
Alcohol should have its’ own tilt category, due to its’ availability in a casino. When players become drunk and start betting more, they not betting more because they’re happy, sad, frustrated, winning, or losing; rather, they’re just betting more because they’re drunk and have a false sense of bravado for no good reason.
The result is the same: player bets more or differently than they would have bet if they had not been drunk.
All forms of tilt do one very dangerous thing: expose more of the bankroll to the house edge.
Tilt acts as amplifier to the house edge. Tilt is an accomplice to the bankroll murder. That’s why in this anatomy of a murder, it’s not proper to solely blame tilt. If the player were to play a positive expectation game, and he started doubling his bet because of loser’s tilt, it would mean that the player would have double the expected gain per bet (assuming the player did not make adverse decisions that reduced his expectation).
It’s not difficult to imagine a craps game – or any casino game – with a positive expectation: just look at the game from the casino’s perspective. The casino is effectively playing craps with a positive expectation. The casino owner might get drunk, make a rash decision and triple his maximum limits. Oh no, the poor casino owner is going to have his clocked cleaned by the martingale bettors. Yea, not really.
Tilt is not a problem until the negative expectation from the house edge is added to the equation.
Let me show you how the house edge and tilt work by breaking down the cost inflicted by the house hedge, and then show you the cost when various levels of tilt is added. Have you ever wondered, ‘what is this hardways bet costing me’?
The House Edge, In Action
Let’s break down the amount of the loss attributable to the house edge.
Let’s say that Gambler Joe likes to play craps, and he is going on vacation. Joe takes a $2o00 bankroll with him. His plan is to play for 4 hours per day, and his vacation is for 5 days in beautiful Las Vegas. In effect, he will play a total of 20 hours of craps during his vacation.
Assuming at the average craps table there will be 100 rolls per hour (note that the Hard Rock Real Craps game, which lasts approximately one hour, has 110 rolls https://youtu.be/7KL8H91s28I). This means that Joe will play about 2000 rolls.
Let’s breakdown his play, and see what it should theoretically cost Joe to play craps on his vacation.
Without tilt and sticking to his normal play
This is how Joe likes to play. Based on my observations at the table, this is a common way for many players to play. So that Joe has a reasonable chance of not being broke in the middle of his vacation, he will bring a $2000 bankroll…
- $10 pass line + $20 odds
- $5 on the hard ways 6 and 8
- $5 craps on the come out
- Place bet of $12 on the 6 and 8
Let’s now do the math on his expected loss per bet over the course of his trip. You can just look to the bold print for the final figure of each bet.
- $10 pass line + $20 odds
- House edge of 1.41% on the pass line, and considering the average number of rolls per pass line bet, the house edge per roll is .42% (citation, Wizard of Odds). We will ignore the odds bet, since there is no house edge. On an expected loss per roll, the expected loss per roll can be broken down into 4.2 cents per roll.
- The average number of rolls for a pass line bet to settle is 3.38 (citation, Wizard of Odds).
- At 100 rolls per hour, his expected loss per hour from pass line betting is $4.20.
- $5 each on the hard ways 6 and 8
- House edge of 9.09%, which is 2.78% per roll, considering it takes on average 3.27 rolls to settle the bet (citation, Wizard of Odds). This works out to an expected loss of 13.9 cents per roll, per number.
- The average number of rolls for a hard ways bet to settle is 3.27 (citation, Wizard of Odds).
- At 100 rolls an hour, his expected loss per hour from betting both the hard ways 6 and 8 is $27.80 ($13.90 per number).
- Note that Joe could reduce his expected hourly losses by turning the hard ways off on the come out.
- $5 Any Craps on the come out
- One roll bet, so the house edge is 11.11% per bet and per roll.
- Since this bet is on the come out only, assuming a new pass line bet every 3.38 rolls, this bet will be made around 29 times in an hour. His expected loss per Any Craps bet is 55.55 cents per roll.
- At 29 Any Craps bets per hour, his expected loss per hour from betting the Any Craps is $16.10
- $12 each on the Place bet of 6 and 8
- House edge is 1.51%, which is .46% per roll, considering the average number of rolls to settle the bet. Thus the expected loss per roll is 5.5 cents per roll, per number.
- The average number of rolls for a Place bet to settle is 3.27 (citation, Wizard of Odds).
- At 100 rolls an hour, his expected loss per hour from betting both the Place 6 and 8 is $11.04 ($5.50 per number).
Expected loss with normal play
Gambler Joe is going to play over 20 hours. This is his expected loss over the vacation for each bet.
- $10 pass line + $20 odds
- Expected loss over the vacation is $84.
- $5 each on the hard ways 6 and 8
- Expected loss over the vacation is $560.
- Note: Now do you understand why the casino allows a $1 or $5 hard ways when the table minimum is $10+?
- Expected loss over the vacation is $560.
- $5 Any Craps on the come out
- Expected loss over the vacation is $322.
- $12 each on the Place bet of 6 and 8
- Expected loss over the vacation is $220.
So the grand total of all his gambling over 5 days is that itcosts Gambler Joe a theoretical $1,186.
If Gambler Joe’s were to cut out the hard ways and the prop betting, his gambling vacation would be relatively cheap at $304.
Even if Joe were to stick to his betting because he loves the hard ways, one could argue that $1,186 as the cost of gambling over a 5-day vacation is not that bad.
So let’s add tilt into Joe’s gambling; not a lot of tilt, just a little.
With mild tilt
While Joe has put a dent into his bankroll, he hasn’t lost his entire bankroll.
This is now the story of how Joe loses his entire bankroll, propping him to consider quitting.
Joe has a bad session or a bad day, and now, he increases his bets.
Joe is not going to play on tilt all of the time. Let’s say that he only goes on tilt, 1/3 of the time (rounded up to 34%). Let’s take his exact play from above, and start increasing his bets because he tilts. Assume 100 rolls per hour, and on 66 of those rolls, he plays his usual game (his ‘normal’ rolls), but he adds to his bet, hoping to chase his losses and bets more (’tilt’ rolls). It doesn’t matter when he presses the bets, because the effect is the same whether he presses in intervals, all at the end, or in the middle of the game.
- $10 pass line + $20 odds
- Tilt causes Joe to increase his pass line bet to $25 because he is at a table that allows a max of 3x, 4x, 5x. He cannot increase his odds without increasing his pass line bet.
- 100 total rolls an hour, of which 66 are normal play, and 34 are on tilt play.
- At 66 normal rolls, expected loss per hour is $2.77
- At 34 tilt rolls, expected loss per hour is $3.57
- At 100 rolls per hour, Joe’s expected loss per hour from pass line betting with tilt is $6.34.
- $5 each on the hard ways 6 and 8
- Joe starts losing or is dazzled by the hard ways constantly rolling in front of him, so he presses or parlays his bets. ‘Parlay’ is when Joe combines the present winnings with the prior bet for the next bet. For example, if a hard 6 rolls and the bet is $5, the payoff is $45; if the player parlays, the hard 6 now has a $50 bet.
- The probability of the hard ways 6 and 8 hitting is 1 in 11 (9.09%), so let’s assume that with 100 rolls an hour, he will hit 9 each of the hard 6 and hard 8. When he hits, he parlays because he can’t stand to miss the possibility of the parlay hitting.
- At 91 normal rolls per hard number, Joe’s expected loss per hour is $25.30 for both the hard 6 and hard 8.
- At 9 tilt/parlay rolls per hard number, Joe’s expected loss per hour is $25.02 for both the hard 6 and hard 8.
- At 100 rolls an hour with tilt, Joe’s expected loss per hour from betting both the hard ways 6 and 8 is $50.32 ($25.16 per number).
- $5 Any Craps on the come out
- Most players who bet the Any Craps on the come out do so to ‘protect’ their pass line bet. In this case, since Joe is pass betting $25 when he is on tilt, let’s just assume that Joe does not increase his Any Craps at all. The payoff of 7-1 is enough to protect his $25 pass.
- At 29 Any Craps bets per hour, Joe’s expected loss per hour from betting the Any Craps is $16.10.
- $12 each on the Place bet of 6 and 8
- Increases on the Place 6 and 8 are likely candidates for increasing bets due to tilt.
- Let’s assume that Joe increases his bets on the place 6 and place 8 to $24 when he goes on tilt, hoping to chase his losses. Each place bet has a probability of winning 46% of the time, so on his losses, which happen 54% of the time, Joe will increase his bet to $24. But let’s not assume that Joe tilts after every loss. Instead, let’s say he only tilts 1/3 of the time when his place bets lose. Thus, only tilting on 18 of his 100 place bet rolls.
- At 82 normal bets per hour, his expected loss per hour is $9.05 for both the place 6 and place 8 bets.
- At 18 tilted rolls per hour, his expected loss per hour is $3.97 for both the place 6 and place 8 bets.
- At 100 rolls an hour, Joe’s expected loss per hour from tilt betting both the Place 6 and 8 is $13.02.
Joes expected loss over his vacation, while playing on on tilt roughly 1/3 of the time, is $1,715.
Even on mild tilt – not steaming raging tilt – Joe has lost almost all of his bankroll.
Press it!
You’ve probably seen the RoadGambler videos, and if you read the comments, one of the most common bits of advice from commenters is to press your bets if they hit.
So let’s see what happens when the bets are pressed.
Note that the reader might think that it’s not proper to account for losses from parlay or presses because that was ‘house’ money. It is not proper to exclude the increases in bets because the money at that point belongs to Joe. Whether the wager comes from the winnings or from the Joe’s own pocket, it makes no difference to the overall calculation.
When making bets, the dice and the laws of probability – and consequently the house edge – do not care if the player used their own money to bet or the casino’s money to make the bet. It’s all the same and does not matter.
Expected losses using the press technique
- $10 pass line + $20 odds
- Player’s usually do not advocate for pressing the pass line bet, so this will remain the same.
- At 100 rolls per hour, Joe’s expected loss per hour from pass line betting is $4.20.
- $5 each on the hard ways 6 and 8
- This is a common candidate for pressing. Let’s say Joe is a jackpot player and likes to parlay. So his first bet is $5, when he hits he will parlay to $50, hoping to win $500 from his original $5 wager.
- If the player plays 100 rolls an hour, and his hard ways are always on, then he will win a 1 and out of 11 attempts on the hard 6 or hard 8 (ten ways to lose, one way to win). This means that 9 of his 100 rolls will have the pressed amount.
- At 91 rolls per hard number, not pressed, Joe’s expected loss per hour is $25.30 for both the hard 6 and hard 8.
- At 9 rolls per hard number that have parlayed bets, Joe’s expected loss per hour is $25.02 for both the hard 6 and hard 8.
- At 100 rolls an hour with parlayed bets, Joe’s expected loss per hour from betting both the hard ways 6 and 8 is $50.32 ($25.16 per number).
- $5 Any Craps on the come out
- Most players do not press the Any Craps, so we will not add a press to this bet.
- At 29 Any Craps bets per hour, Joe’s expected loss per hour from betting the Any Craps is $16.10
- $12 each on the Place bet of 6 and 8
- This is the bet most likely to be pressed, and players will routinely press this bet three or four times or more. For purposes of this calculation, let’s press the bet three times.
- 100 total rolls, the player will win 46% of his rolls roughly, and of that 46% will win, and 46% of that.
- Out of 100 total rolls involving a place bet of 6 and 8, the following is the approximate number of rolls for each press
- 54 rolls, on average, involve bets that are never pressed and stay at $12
- expected loss per hour for both numbers is $5.96
- 25 rolls, on average, involve bets that are pressed only once (lose before the second press occurs) and thus are pressed to $24
- expected loss per hour for both numbers at this press level is $5.52
- 11 rolls, on average, involve bets that are pressed twice (lose before the third press) and are thus pressed to $48
- Expected loss per hour for both numbers at this press level is $4.85
- 10 rolls, on average, involve bets that are pressed three times (this level is similar to the above level because no bets are pressed if the number hits) and are thus wagered at $96.
- Expected loss per hour for both numbers at this press level is $9.71
- 54 rolls, on average, involve bets that are never pressed and stay at $12
- Out of 100 total rolls involving a place bet of 6 and 8, the following is the approximate number of rolls for each press
- At 100 rolls an hour, Joe’s expected loss per hour from place betting both the 6 and 8 and pressing each win 3 times is $26.04.
Thus when we add up all the expected losses and add the advice to press numbers, using the same parameters as Gambler Joe on his vacation, the expected loss over the vacation is now $1,933.
Joe has practically busted his entire bankroll. If anything, Joe has done more damage to his bankroll by pressing his wins than if he had followed his milder tilt desires.
This is why the RoadGambler rarely presses bets, unless it’s done to entertain the viewer, which is an overarching goal of the Real Craps Series.
I’m not saying to never press bets. It’s ok to press bets because, in the end, it’s sometimes fun to press; however, it’s another thing to press thinking that pressing will give the player an advantage because certain numbers appear to be ‘hot’. The dice do not know how many times any number has rolled. The justification that a number is more likely to roll because the table is hot is just pure Gambler’s Fallacy: https://en.wikipedia.org/wiki/Gambler%27s_fallacy
Theoretical Probability Of Winning Craps Against
Note that the above play is rather conservative: pass line with odds, one prop bet, a place bet on the 6 and 8, and a pair of hard ways bets on the 6 and 8. If the player adds other bets, such as the ‘Yo’ or covers all the hard ways, it gets way worse.
Add something like the World bet on a regular basis, and you will lose so regularly that you’ll question why you play craps at all.
Beserker’s tilt, aka crazy tilt
Many gambler’s have seen this form of tilt. It’s when the player goes on a rampage and presses or increases his bets significantly beyond what he would normally bet. He’s not just chasing his losses and increases his bets to outsized proportions.
- $10 pass line + $20 odds, increased to $50 pass
- Tilt causes Joe to increase his pass line bet to $50 and he can’t stop. In addition to increasing his bet he also stays at the table much longer, refusing to leave because he’s down. So his number of hands played at the higher amount balloons. Because all of this additional time at the table is tilted, 75% of his play is tilted.
- 100 total rolls an hour, of which 66 are normal play, and 34 are on tilt play.
- At 25 normal rolls, expected loss per hour is $1.15.
- At 75 tilt rolls, expected loss per hour is $17.25
- At 100 rolls per hour, Joe’s expected loss per hour from pass line betting with berserker tilt is $18.14.
- $10 each on all the hard ways.
- Joe starts is super tilted because he has been losing, has been seeing the 4 and 10 hit, and now covers all the hard ways and at $10 each, parlaying each bet.
- The probability of hitting the hard way 6 and 8 is 1 in 11 (9.09%), so let’s assume that with 100 rolls an hour, he will hit 9 each of the hard 6 and hard 8. When he hits, he parlays.
- At 91 normal rolls per hard number, Joe’s expected loss per hour is $50.60 for both the hard 6 and hard 8.
- At 9 tilt/parlay rolls per hard number, Joe’s expected loss per hour is $50.04 for both the hard 6 and hard 8.
- At 100 rolls an hour with berserker tilt, Joe’s expected loss per hour from betting both the hard ways 6 and 8 is $100.64
- The probability of the hardways 4 and 10 hitting is 1 in 9 (11.11%), so let’s assume that with 100 rolls an hour, he will hit 9 each of the hard 4 and hard 10. When he hits, he parlays.
- At 89 normal rolls per hour on hard 4 and 10, Joe’s expected loss per hour is $49.04 for both the hard 4 and 10.
- At 11 tilt/parlay rolls per hard number, Joe’s expected loss per hour is $61.16 for both the hard 4 and 10.
- At 100 rolls an hour with berserker tilt, Joe’s expected loss per hour from betting the hard 4 and 10 is $110.20.
- Joes expected loss from covering all the hardways and parlaying one time is a staggering $210.84 per hour.
- $5 Any Craps on the come out
- Most of the time, drop any thought of ‘protecting’ their come out roll once they’re on crazy tilt.
- $96 each on the Place bet of 6 and 8
- Increases on the Place 6 and 8 are likely candidates for increasing bets due to tilt.
- So Joe increases his place bet to $96 per number for the second half of his vacation because he’s really trying to chase.
- At 100 rolls an hour, his expected loss per hour from betting both the Place 6 and 8 is $88.32
- But no one plays on tilt the entire time, as there must be some sort of stimulus that triggers the tilt. So let’s say half the time, Joe is not on tilt, so the expected loss from this tilted bet is $44.32 per hour.
Joes expected loss per hour is a staggering $273.30

Added all up, over five days of vacation, if Joe goes on crazy berserker tilt, his expected loss is $5,466.
Want to know something else that’s scary? If you regularly play at that level and make those bets and parlays, you will have the same expected losses…without tilt!
Even if you remove the $96 place bet on the 6 and 8 and stick to the smaller $10 bets on the hard ways cover all, your expected loss over the same vacation will still be a relatively high $4,579.
Do you still wonder why you go home broke?
CONCLUSION
I have many conversations with gamblers. I’ve heard every reason why a player loses, many will admit to tilt; but I do not recall the last time that I heard someone say, ‘I lost because of the house edge’.
In the end, the direct cause of all losses is directly traced back to one culprit: the house edge that is built into the game. Tilt is then the amplifier – the executioner – that comes in and finishes your bankroll.
This is the final take away from Part 2:
The dice and the laws of probability do not know or care that bet was made by a drunk person, an angry person, a happy person, a mad person, a person who had just lost a bet, a person who had just won a bet, an old person, a young person, a virgin shooter, etc.
The laws of probability coldly dictate that on the next roll, a 12 bet has 1 way to win and 35 ways to lose, and the casino knows that to make a profit, the casino must pay less than true odds, so it pays 30-1. That’s how the house edge is applied.
Really, that’s the only reason why any gambler loses. Then, if the gambler becomes tilted, his losses will increase significantly.
But there’s hope…
In Part 3, we will discuss how to control the house edge and control tilt. Doing so will help you deal with your losses and maximize your wins.
The house edge might be an unavoidable statistical reality, but large ruinous losses do not need to be inevitable.
You can win.
You just need to identify the real culprits of this bankroll murder so that you can be on guard against them. Otherwise, you’ve identified the wrong suspects, and the crime will continue.
Posted in: Blackjack, Casino, Craps, Gambling
The majority of casino games are known to offer either a low or a high house edge. Craps stands out from the crowd because it offers both. For one thing, this unique game features some of the best bets you can possibly make in a casino. For another, some of the more advanced, proposition bets in craps give the house a formidable edge over patrons that nearly reaches 17%!
Another distinctive trait of craps is that it is the only game of chance where players can actually bet something will not happen instead of backing the outcome they believe is most likely to occur, as is the case with Don’t Come and Don’t Pass bets.
These two features are what render this simple game of chance so unique and appealing in the eyes of millions of gamblers around the world.
As simple as craps seemingly is, you most definitely should take the time necessary to learn all the possible dice combinations along with their odds and probabilities before you invest any of your money in the game.
The purpose of this part of the guide is to introduce you to all dice combinations in craps and to help you make a distinction between true and casino odds. By the end, you will know whether dice control is effective in reducing the house edge and will be able to calculate your average expected losses at the craps tables.
Possible Dice Combinations in Craps
As we have previously explained in this guide, craps is a game of chance that plays with two six-sided dice, with each side having a different number of pips so as to represent numerical values 1 through 6. Each toss of the two dice can result in one of 11 possible numbers, namely numbers 2 through 12.
When two dice are in play, the number of possible dice combinations increases to 36 since each dice is practically a cube with six sides (6×6 = 36). Now, we want you to take a closer look at the table below and see whether you will be able to notice a trend.
| Dice Total | Number of Ways to Throw Total | Possible Combinations |
|---|---|---|
| 2 | 1 | 1-1 |
| 3 | 2 | 1-2, 2-1 |
| 4 | 3 | 1-3, 3-1, 2-2 |
| 5 | 4 | 1-4, 4-1, 2-3, 3-2 |
| 6 | 5 | 1-5, 5-1, 3-3, 2-4, 4-2 |
| 7 | 6 | 1-6, 6-1, 2-5, 5-2, 3-4, 4-3 |
| 8 | 5 | 2-6, 6-2, 5-3, 3-5, 4-4 |
| 9 | 4 | 3-6, 6-3, 4-5, 5-4 |
| 10 | 3 | 4-6, 6-4, 5-5 |
| 11 | 2 | 5-6, 6-5 |
| 12 | 1 | 6-6 |
You have probably noticed the column with the possible combinations is diamond-shaped. From this shape, it becomes apparent the number of combinations that may result in a toss of 7 is the highest, which automatically means the probability of this number being tossed is the highest.
As many as 6 combinations result in a 7 which is the main reason why the majority of seasoned craps players favor the Pass Line where a come-out roll wins when 7 or 11 are tossed, with a total of 8 possible winning combinations (six for a toss of 7 and two more for a toss of 11).
Do not be intimidated by the chart – there is one easy way for you to learn the combinations by heart. All you have to do is use 7 as a starting point and divide the remaining outcomes into groups of two. You can pair rolls of 6 and 8 since both outcomes have 5 possible combinations.
Next in line is the pair of 5 and 9, with each of these rolls having 4 possible combinations. The next pair comprises rolls of 4 and 10 with three dice combinations. Then you have 3 and 11 where the number of possible combinations drops with a unit to two.
The rolls of 2 and 12 are the easiest to memorize since there is only one possible dice combination for each of the two outcomes. Learning these combinations is essential because it helps you gain a better understanding of the odds and probabilities in craps. We tackle the subject in the next section.
Understanding the Odds and Probabilities of Craps Bets
This is the part most gamblers struggle with. Craps, like all other games of chance, is based on independent trials, which is to say the odds of the dice rolls remain constant and are not influenced by previous outcomes. This is easily the most important aspect of the game all craps players must understand. Yet, there are people who would invest their action in a given dice outcome simply because they have not seen it occur in a while.
Here it is important to draw a distinction between odds and probabilities. While interrelated, the two terms do not denote one and the same thing as many gamblers mistakenly presume. Probability is nothing more than the likelihood of an independent outcome occurring and is usually expressed either as a proper fraction or as a percentage.
To calculate the probability of rolling a certain value, you must know the number of dice combinations that result in it as well as the number of all possible dice combinations. For instance, the probability of tossing a 7 on the come-out roll is the highest at 16.67%. We can also say the probability is 6 in 36 because there are 6 winning combinations out of 36. This is called theoretical probability.
Odds, on the other hand, show you the ratio between winning and losing outcomes and are usually expressed as fractions. So for example, if you decide to make a Snake Eyes bet, which is a wager on a single roll of 2, the odds of winning will be 1 to 35 because there is only one winning combination for this roll while the remaining 35 combinations result in a loss. This corresponds to a theoretical probability of 2.78% because 1/36 = 0.02777 x 100 = 2.78%. Consult the table below to see the probabilities of rolling all two-dice totals in craps.
| Two-Dice Total | Probability as a Fraction | Probability of Rolling the Total as a Percentage |
|---|---|---|
| 2 | 1/36 | 2.78% |
| 3 | 2/36 | 5.55% |
| 4 | 3/36 | 8.33% |
| 5 | 4/36 | 11.11% |
| 6 | 5/36 | 13.89% |
| 7 | 6/36 | 16.67% |
| 8 | 5/36 | 13.89% |
| 9 | 4/36 | 11.11% |
| 10 | 3/36 | 8.33% |
| 11 | 2/36 | 5.55% |
| 12 | 1/36 | 2.78% |
The Difference between True Odds and Casino Odds
It is of essential importance for you to understand there is a distinction between true odds and casino odds. It is the discrepancy between the two that gives the house the edge that eventually grinds the bankrolls of imprudent gamblers down to nothing.
If you hang around a casino for an hour or so, you are more than likely to hear (losing) players complaining about the games being rigged as they exit the venue with empty pockets. These players are, in fact, correct to a certain extent. The games are indeed rigged against them but not because the casino resorts to cheating. Why cheat your patrons when there is a perfectly legal way of extracting their money?
Another Example
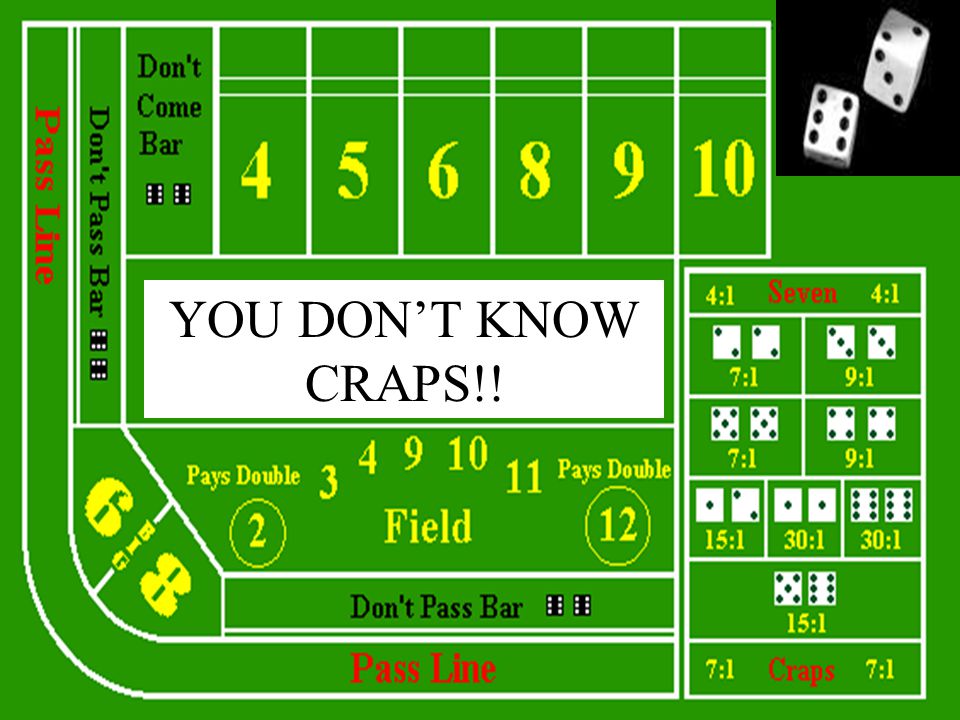
The main reason gamblers lose in the long term is the above-mentioned discrepancy between true odds and the odds the house pays you at when you win. The following example demonstrates how the house edge in craps works. Let’s presume you decide to make 36 consecutive Snake Eyes bets wagering a dollar on each. The mathematically correct odds for this bet are 35 to 1, which is to say 35 of all possible combinations result in a loss whereas only 1 combination (1-1) can lead to a win.
Now take a quick glance at the layout of the craps table. Can you see what it says? The payout for a one-roll Snake Eyes bet on 2 is 30 to 1 instead of being 35 to 1, as it should be. The same goes for a roll of 12 where again there is a single winning combination (6-6). This applies to all payouts in craps – they have all been reduced, making it possible for the house to extract consistent profits from its tables in the long term.
So you wager a dollar on Snake Eyes a total of 36 times in a row and the results are mathematically perfect, meaning that one of those 36 trials was indeed a winning one. Now, this is unlikely to happen in the short term but generally, the more you play, the closer your results get to the mathematical expectations for the game.
Players can easily figure out what the house edge is for any available bet in craps as long as they know its true odds, its payout, and its probability. Let’s demonstrate how this works for the Any 7 bet. This wager wins on a roll of 7, regardless of which one of its six combinations occurs. The payout for a winning Any 7 bet is 4 to 1. The probability is 6 in 36 possible dice combinations.
The calculations will run in the following manner: (6/36) x 4 – (30/36) = (0.166 x 4) – 0.833 = 0.666 – 0.833 = (-0.166) x 100 = -16.67. The figures in the first brackets correspond to the probability of winning with an Any 7 bet, which is then multiplied by the casino’s payout of 4 units per unit wagered. You then subtract the probability of losing (the figures in the second brackets stand for 30 ways to lose out of 36 possible combinations) from the result and get a house edge of 16.67% for the Any 7 bet.
As you can see, you will lose $16.67 (hence the “-”) per every $100 wagered on the Any 7 bet. In other words, your expected return with this bet will be in the negative at -$16.67. If you are still struggling to understand this, we suggest you go back to the Craps House Edge article of this guide where you will be able to find further explanations on the matter along with the true and casino odds of all available craps bets.
Distinguishing between “To” and “For” Odds
The trouble with most casual gamblers is that they are so engulfed in the action, they rarely pay any attention to anything else, including what’s in front of their eyes, right there on the table layout. If you take the time to carefully inspect craps layouts, you will undoubtedly notice there is something weird about the proposition bets section at some craps tables.
In some casinos, the layout states that you get 5 units “for” 1 unit wagered on Any 7 instead of the usual payout of 4 “to” 1. The same goes for proposition bets like the Hard 6 and the Hard 10 which pay 10 unit for each unit wagered instead of the usual 9 to 1. Many undiscerning gamblers are misled by this phrasing (that was the purpose in the first place) and are quick to assume their winning proposition bets return at enhanced odds. There is nothing of the kind, though.
Theoretical Probability Of Winning Craps Games
The “for” payouts are basically the same since they include your initial stake. In contrast, the phrasing “to” distinguishes your net profits from your original bet. So in the case of the Any 7 bet, you get 4 units in net profits plus your original stake of 1 unit for a total of 5 units.
The wording of these payouts is no coincidence. Quite the contrary, the house uses this sly approach for the purpose of leading inexperienced craps players into believing they get higher payouts on the wagers with the steepest house edge when in reality, they are paid at standard casino odds. No matter what phrasing is used, we would like to remind you not to waste your money on proposition bets. The monstrous house edge you combat with these wagers is not worth it even if the payouts were indeed “enhanced”.
Figuring Out Your Expected Loss in Craps
This section is somewhat a continuation of the True Odds one. You are probably scratching your head wondering why on earth would we teach you how to calculate your expected losses. What you want to know is how to determine your hourly expected profits, right? We hate to break this to you but craps is a negative expectation game which is to say your expected value in the long run will always be in the negative due to the house edge, i.e. you will inevitably lose money to the casino in the long term.
It is important for you to learn to calculate your expected loss so that you know at what average rates you will lose money per hour. This depends on your action, the types of bets you make, and their house edge. The formula is quite simple – you must multiply the number of rounds you play per hour by the amount you wager, the house edge, and the number of hours you intend to play.
So, let’s suppose you play at a slower pace and go through 160 rolls, betting $5 on Any 7 for one hour. The calculations will look like this: 160 x $5 x 0.166 x 1 = $133 on average. This is the average rate at which you lose money with Any 7 wagers but you arrive at this amount after a gazillion of independent trials. In the short term, you might end up losing much more or far less within an hour. The bottom line is the longer you play, the closer you get to these expected loss figures.
Can Dice Control Influence the Probability of Rolling Certain Combinations?
Some craps players would attempt to influence the outcome of the rolls by using an advanced technique, called dice setting or dice control. The main idea here is that you can skew the odds in your favor by tossing the dice in a specific manner. To achieve this, the shooter must toss the dice at the correct angle in order to allow them to produce the desired outcome.
The toss itself should be performed with as little hand movements as possible so that the dice do not tumble as much before they hit the back wall of the craps table. The dice must be picked in a particular way as well. The shooter’s wrist remains locked during the toss, i.e. there is no twisting motion when the dice are thrown. It makes sense this technique takes ages to master but the real question is does it really help you influence the outcome of the roll?
Theoretical Probability Of Winning Craps Rules
Renowned gambling author Stanford Wong is among the proponents of the efficiency of this technique and wrote extensively about it in his book Wong on Craps. The subject was also tackled by author Christopher Pawlicki in his 2002 book Get the Edge at Craps: How to Control the Dice. Some mathematicians and gambling experts are of the opinion the technique either does not work or is impossible to execute successfully in the casino environment.
Theoretical Probability Of Winning Craps Odds
Others are willing to give dice control some credence arguing that it might possibly work, provided that the dice do not hit the back wall of the craps table. Unfortunately, most casinos require the dice to hit the back wall in order for the roll to be considered valid. The bottom line is most members of the advantage play community still distrust the concept of overcoming the house edge in craps through dice control.